Pengertian Bilangan Prima
Bilangan prima adalah bilangan asli yang bernilai lebih dari 1 dan mempunyai 2 faktor pembagi yaitu 1 dan bilangan itu sendiri. Dengan menggunakan pengertian bilangan angka prima tersebut, kita dapat memahami bahwa angka 2 dan 3 merupakan bilangan prima, karena hanya bisa dibagi dengan angka satu dan angka itu sendiri.
Dalam matematika, bilangan prima adalah bilangan asli yang lebih besar dari angka 1, yang faktor pembaginya adalah 1 dan bilangan itu sendiri. 2 dan 3 adalah bilangan prima. 4 bukan bilangan prima karena 4 bisa dibagi 2.
Jika suatu bilangan yang lebih besar dari satu bukan bilangan prima, maka bilangan itu disebut bilangan komposit. Cara paling sederhana untuk menentukan bilangan prima yang lebih kecil dari bilangan tertentu adalah dengan menggunakan saringan Eratosthenes. Berikut adalah 168 bilangan prima pertama (semua bilangan prima kurang dari 1000):
- 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997 (barisan A000040 pada OEIS).
Baca Juga Artikel Yang Mungkin Berhubungan : Contoh Bilangan Cacah Lengkap
Sejarah Bilangan Prima
Manusia telah mengenal bilangan prima scjak 6500 sebclum maschi (S.M.). tulang Ishango yang ditcmukan pada tahun 1960 (sckarang disimpan di Musse d’Histoire Naturelle di Brussels) mcmbuktikan hal tersebut. Tulang Ishango memiliki 3 baris takik. Salah satu kolomnya memiliki 11, 13, 17 dan 19 takik, yang merupakan bilangan prima antara 10 dan 20.
Sekitar abad 6 S.M., Phythagoras dan kelompoknya telah mempelajari sifat-sifat bilangan, antara lain : bilangan sempurna (perfect numbers), bilangan sekawan (amicable numbers), bilangan segi banyak(polygonal numbers) dan bilangan prima (prime numbers). Sclanjutnya, sekitar abad ke empat SM, Euelides mengembangkan konsep dasar teori bilangan. Beberapa jenis bilangan khusus akan dikemukakan, namun pengertian pembagi dan pcmbagi sejati perlu dikemukakan lebih dahulu.
Pcmbagi (kadang disebut faktor) dari sebuah bilangan bulat adalah bilangan yang dapat mcmbagi bilangan itu tanpa adaa sisa. Misalnya pcmbagi dari 12 adalah . Pcmbagi scjati (proper divisors) adalah pcmbagi sebuah bilangan yang kurang dari bilangan itu sendiri. Misalnya pcmbagi scjati dari 12 adalah . Sclanjutnya, beberapa bilangan khusus dikemukakan sebagai berikut :
- Bilangan Berlimpah (Abundant Numbers)
Jika sebuah bilangan dengan jumlah pcmbagi scjatinya lebih dari bilangan itu scndiri discbut bilangan berlimpah. Misalnya, pcmbagi sejati 24 adalah dan l+2+3+4+6+8+12-36 adalah bilangan berlimpah karena 36>24. - Bilangan Berkckurangan (Deficient Numbers)
Jika jumlah pembagi scjati scbuah bilangan kurang dari bilangan itu sendiri, maka bilangan itu disebut berkckurangan. Misalnya, 16 adalah bilangan berkckurangan karena jumlah pembagi sejatinya adalah 1 +2+4+8= 1 < 16. - Bilangan Scmpurna (Perfect Numbers)
Scbuah bilangan disebut scmpurna apabila jumlah pembaginya sama dengan bilangan itu sendiri. Misalnya, 6 adalah bilangan scmpurna karena pembagi 6 adalah 1,2 dan 3 serta 1+2+3=6. - Bilangan Mungil (cute numbers)
Jika scbuah bilangan kuadrat dapat dibagi ke dalam n kuadrat pada paling banyak dua ukuran berbeda, maka n disebut bilangan mungil. Misalnya 4 dan 10 adalah bilangan mungil. - Bilangan Setcngah Sempurna (semiperfect numbers)
Sebuah bilangan setcngah sempurna apabila sama dengan jumlah sebagian pembagi sejatinya. Misalnya, misalnya 18 adalah bilangan setcngah sempurna karena pembagi sejati 18 adalah dan 3+6+9-18. Sebuah bilangan setcngah sempurna yang merupakan jumlah dari semua pembagi sejatinya disebut bilangan sempurna. - Bilangan Berbahagia (happy numbers)
Sebuah bilangan yang jumlah kuadrat angka-angkanya pada akhirnya berjumlah satu disebut bilangan berbahagia. Misalnya 203 adalah bilangan berbahagia, karena + + =13, + =10, + =1. - Bilangan Narsis (narcissistic numbers)
Seorang narsis jika tertarik kepada dirinya sendiri, scbuah bilangan narsis nampaknya sedikit terpusat pada dirinya juga. Scbuah bilangan narsis adalah scbuah bilangan yang sama dengan scbuah pernyataan yang menggunakan angka yang sama. Misalnya 36= 3! 6. Kadang-kadang scbuah bilangan narsis didefenisikan sebagai bilangan yang sama dengan jumlah angka- angkanya yang berpangkat tertentu. Lebih khusus, scbuah bilangan dengan n angka sama dengan jumlah angka-angkanya yang berpangkat tertentu. Lebih khusus, scbuah bilangan dengan n angka sama dengan jumlah angka-angkanya berpangkat n. Misalnya, 371 adalah bilangan narsis karena 371= dan 9474 juga bilangan narsis karena - Bilangan Palindrom (palindromic numbers)
Scbuah polindrom adalah kata yang sama baik dibaea dari kiri maupun kanan, misalnya noon atau kayak. Bilangan polindrom, seperti 88 dan 1640461 mempunyai angka yang sama baik dibaea dari kiri maupun dari kanan. - Bilangan Palindrom {palindromic numbers)
Scbuah polindrom adalah kata yang sama baik dibaca dari kiri maupun kanan, misalnya noon atau kayak. Bilangan polindrom, sepcrti 88 dan 1640461 mcmpunyai angka yang sama baik dibaca dari kiri maupun dari kanan. - Bilangan bcrsahabat {amicable numbers)
Dua bilangan disebut bcrsahabat apabila jumlah pcmbagi scjati bilangan pcrtama sama dcngan bilangan kedua dan juga sebaliknya jumlah pcmbagi scjati bilangan kedua sama dcngan bilangan pcrtama. Misalnya, 2620 dan 2924 adalah dua bilangan bcrsahabat. Pcmbagi scjati 2620 adalah yang jumlahnya .
Selanjutnya, kita mcmeriksa pcmbagi scjati 2924, yaitu dan jumlahnya . Dcngan dcmikian, kedua bilangan itu bcrsahabat. - Bilangan Sosial (sociable numbers)
Bilangan sosial scpcrti bilangan bersahabat, tctapi bilangan sosial dalam kelompok yang lebih besar. Pcmbagi sejati dari bilangan pertama dalam scbuah kelompok jumlahnya sama dcngan bilangan kcdua, pcmbagi sejati bilangan kedua jumlahnya sama dcngan bilangan ketiga, dan sctcrusnya. Pcmbagi sejati bilangan terakhir dalam kelompok jumlahnya sama dcngan bilangan pertama. Bilangan sosial cenderung besar, schingga sulit didapatkan tanpa menggunakan komputer. Satu contoh kelompok bilangan sosial adalah 12496, 14288, 15472, 14536 dan 14264. - Bilangan Berpola (figurate numbers)
Bilangan dari titik dalam scbuah susunan titik-titik yang berjarak sama disebut bilangan berpola. Misalnya: Titik-titik dapat disusun dalam dimensi satu, dua, tiga atau lebih. Ada banyak jenis bilangan berpola, misalnya bilangan polygon (polygonal numbers) dan bilangan tetrahedral (tetrah edra l mini bers). - Bilangan Poligon (polygonal numbers)
Sebuah bilangan poligon adalah bilangan titik yang berjarak sama dipcrlukan untuk mcnggambar sebuah bilangan bcrpola. Barisan bilangan poligon berdasarkan pada poligon tersarang. Contohnya:
banyak jenis berbeda dari bilangan poligon, mulai dengan bilangan kuadrat dan bilangan segitiga. - Bilangan Kuadrat (square numbers)
Bilangan kuadrat adalah hasil perkalian sebuah bilangan dengan dirinya sendiri. Ini adalah sama dengan kuadrat sempuma (perfect squares): =1, =4, =9 dan seterusnya. Kuadrat dari 5 adalah 25 dan bekerja dari belakang, kita mengatakan bahvva akar kuadrat dari 25 adalah 5. Beberapa gambar bilangan kuadrat diberikan sebagai berikut. - Bilangan Kubik (cube numbers)
Bilangan kubik adalah hasil dari pcrkalian scbuah bilangan dcngan dirinya scndiri dua kali : = 1, =8, =27 dan seterusnya. Kubik dari 4 adalah 64 dn bekcrja dari bclakang, kita mcngatakan bahwa akar pangkat tiga dari 64 adalah 4. Jika kita menggunakan balok bentuk kubik (kubus) untuk membangun scbuah kubik lcbih besar, banyaknya balok yang diperlukan adalah scbuah bilangan kubik. Misalnya, kita akan membangun kubik 10 cm dcngan menggunakan kubik 1 cm kita membutuhkan 1000 kubik. - Bilangan Tetrahedral (tetrahedral numbers)
Bilangan tetrahedral adalah satu jenis bilangan berpola yang diperoleh dcngan menghitung banyaknya titik berjarak sama yang diperlukan untuk membangun scbuah tetrahedron. Tetrahedron adalah piramid dcngan dasar segitiga.
Baca Juga Artikel Yang Mungkin Berhubungan : Sistem Bilangan Biner
Rumus Bilangan Prima
Selama bcrabad-abad, banyak matematikawan telah mcncoba untuk mencari rumusan yang dapat digunakan dalam mcnentukan bilangan prima. Scmua bilangan prima yang lebih besar dari 2 jclas mcrupakan bilangan gasal (ganjil) schingga orang pcrcaya bahwa untuk suatu bilangan prima p,-1 juga mcrupakan bilangan prima. Persamaan ini sama halnya dengan persamaan yang diungkapkan olch Mersenne, yakni minus: – -1, n>l. Namun, hal tersebut kemudian terbukti tidak bcnar. Pada tahun 1536, Regius membuktikan bahwa bilangan -1=2047=23 89, bukan bilangan prima.
Cara yang paling sederhana untuk mencari bilangan prima adalah dengan menggunakan metode saringan Eratosthenes (Sieve of Eratosthenes), scbuah karya dari Eratosthenes (240 SM), seorang ilmuwan Yunani Kuno. Cara ini yang paling sederhana dan paling eepat untuk menemukan bilangan prima, sebelumsaringan Atkin ditemukan pada tahun 2004. Saringan Atkin mcrupakan cara yang lebih eepat namun lebih rum it dibandingkan dengan saringan Eratosthenes.
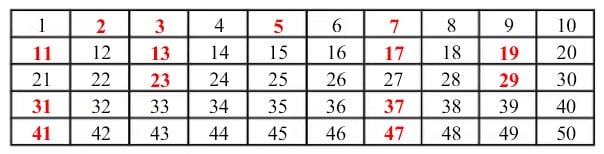
Misalkan, kita hendak menemukan semua bilangan prima di antara 1 sampai bilangan bulat 50. Peragaaun saringan Eratosthenes untuk membuat daftar bilangan kurang dari atau sama dengan 50 dilakukan sebagai berikut:
- Membuat daftar bilangan mulai dari 1 sampai dengan 50,
- Mencoret bilangan I dari daftar bilangan tcrscbut.
- Membiarkan bilangan 2 dan mcncorct scmua bilangan kclipatan 2,
- Membiarkan bilangan 3 dan mcncorct scmua bilangan kclipatan 3,
- Membiarkan bilangan 5 dan mcncorct scmua bilangan kclipatan 5,
- Membiarkan bilangan 7 dan mcncorct scmua bilangan kclipatan 7,
- Membiarkan scmua bilangan yang belum dicorct,
- Melihat hasil bilangan yang dibiarkan dan tidak dicorct.
- Mendaftar scmua bilangan prima yang kurang dari 50, yaitu 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31,37,41,43 dan 47.
(catatan: bcbcrapa bilangan mcndapat pcncoretan Icbih dari sckali)
Penggunaan saringan Eratosthenes tidak dapat secara memuaskan untuk mcnguji langsung suatn bilangan adalah bilangan prima atau bukan bilangan prima, sehingga banyak ” formula ” lain yang dibuat untuk mcnghasilkan bilangan prima. Rumus atau formula itu antara lain:
- f(n)= -n+41, untuk n N
Untuk n=l sampai dcngan n=40, dipcroleh daftar angka yang merupakan bilangan prima. Tctapi, untuk n=41 maka f(41)= bukan bilangan prima karena 1681 habis dibagi 1,41 dan 1681. Dcngan dcmikian, f(n)= -n+41 gagal menjadi rumus bilangan prima. - f(n)= -79n+1601
Formula ini gagal menjadi rumus bilangan prima sebab f(81)= -79(81)+1601_1763, di mana faktor dari 1763 adalaah 1,41,43 dan 1 763, sehingga 1763 bukan bilangan prima. - f(n)= +1
Rumus ini dibuat oleh Fermat. Jika seeara berturut-turut n diganti dcngan 1,2, 3 dan 4 maka dipcroleh semuanya adalah bilangan prima. Tctapi, jika n diganti dcngan 5 maka f(5)=+ 1-4.294.967.297. Hasil ini bukan bilangan prima karena habis dibagi oleh 641. Jadi, rumus Fermat gagal menghasilkan bilangan prima untuk n=5. - Bilangan prima Sophie Germain.
Sebuah bilangan prima p discbut bilangan prima Sophie Gennain bila 2p+l juga bilangan prima. Misalnya, 23 adalah bilangan prima Sophie Germain karena 2 23+1=47 juga bilangan prima. Bilangan ini diberi nama sesuai nama matematikavvan Perancis Marie Sophie Germain. - Bilangan prima dcngan rumus 3+4k.
untuk k>0. Tentu, rumus ini gagal menghasilkan bilangan prima untuk k=3, karena 3+4(3)=15 bukan bilangan prima. - Teorema kccil Fermat
menyatakan jika p cidcilah bilangan prima, maka untuk semuci bilangan bulat a, =a(mod p). Ini berarti, jika kita mengambil sembarang bilangan a, kemudian mengalikan dcngan dirinya sendiri sebanyak p kali dan mengurangi a, hasilnya akanhabis dibagi dcngan p.
Secara khusus, jika a bukan faktor p, maka (mod p) 1. Teorema ini memberikan uji yang baik untuk ketidakmiripan. Dcngan bilangan bulat n>l, pilihlah a>l dan hitung (mod n). jika hasilnya 1, maka n bukan bilangan prima. Scbaliknya, jika hasilnya=l, maka n mungkin bilangan prima schingga n mungkin disebut bilangan prima semu basis a (prima semu, bilangan yang “mendekatr bilangan prima).
Scbagai contoh, untuk a=2 dan n=341, maka (mod 341)= (mod 341)= = mod 341— 1. Tctapi, 341 bukan bilangan prima karena 341= , schingga 341 adalah bilangan prima semu basis 2. (umumnya digunakan oleh praktisi kriptografi, kriptografi adalah teknik untuk menyamarkan suatu pesan dcngan kata lain “sandi”).
Mcski bilangan prima Merscnnc terbukti tidak secara pasti benar bahvva rumus tersebut adalah rumus untuk bilangan prima, namun para pcneliti tetap menggunakan rumus Merscnnc dalam mencari bilangan prima. Bilangan prima terbesar yang diketahui pada September 2006 adalah -1. Bilangan ini mempunyai 9.808.358 digit dan merupakan bilangan prima Mersenne yang ke-44. (demikian notasi penulisan bilangan prima Mersenne ke-44) ditemukan oleh Curtis Cooper dan Steven Boone pada 4 September 2006 yang keduanya adalah profesor university ofSentral Missoouri bekerja sama dengan puluhan ribu anggota lainnya dari proyek Great Internet Mersenne Prime Search (GIMPS).
Di antara semua bilangan prima Mersenne yang sudah ditemukan, sepuluh bilangan terbesarnya ditemukan 9.808.358 digit angka.
Baca Juga Artikel Yang Mungkin Berhubungan : Pengertian Bilangan Rasional beserta Sifat dan Contohnya
Contoh Bilangan Prima dari 1 Sampai 100

Siapa yang tidak akrab dengan bilangan prima? Di dalam pelajaran Matematika ada yang namanya materi bilangan prima. Tidak sulit sebenarnya asalkan mau mempelajari dengan baik. Karena kita hanya perlu memahami dan sedikit menghafal. Bagi kalian yang masih SD, bahkan sampai perguruan tinggi negeri materi ini mungkin masih diajarkan. Dan apabila kalian ingin mempelajari lebih lanjut mengenai bilangan prima, maka marilah belajar bersama-bersama.
Bilangan prima adalah bilangan asli lebih besar dari 1 dan hanya bisa dibagi 2 bilangan yaitu 1 serta bilangan itu sendiri. Angka 2 dan 3 juga dinyatakan sebagai bilangan prima sedangkan angka 4 bukanlah bilangan prima karena dapat dibagi dengan angka 2.
Sepuluh bilangan prima pertama yaitu ada 2, 3, 5, 7, 11, 13, 17, 19, 23. Jika sebuah bilangan besarnya lebih dari satu dan buka bilangan prima maka dinyatakan sebagai bilangan komposit.
Faktor prima suatu bilangan yakni bilangan prima di faktor bilangan itu sendiri. Langkah guna mencari faktor prima suatu bilangan adalah dengan menggunakan pohon faktor. Contohnya temukan faktor prima dari 14 dan 40. Maka bilangan yang akan dicari faktornya dibagi menggunakan bilangan prima.
Jika masih dibagi dengan bilangan prima lainnya, maka bagilah, dan faktor prima dari 14 yaitu 2 x 7 sedangkan faktor prima dari 40 adalah 2 x 2 x 2 x 5.
- Bilangan prima dari 1 sampai 100 yakni 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
Bilangan prima dari 1 sampai 100, prima terbesar sebenarnya tidak ada karena jumlah itu tidak terhingga.
- Bilangan prima tiga digit pertama : 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 163, 167, 173, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263.
- Bilangan prima empat digit pertama : 1009, 1013, 1019, 1021, 1031, 1033, 1039, 1049, 1051, 1061, 1063, 1069, 1087, 1091, 1093, 1097, 1103, 1109, 1123, 1129, 1153, 1163, 1171, 1181.
Contoh soal dari bilangan prima dari 1 sampai 100 adalah sebagai berikut:
Berapakah bilangan prima antara 1 hingga 10?
Jawabannya adalah 2, 3, 5, 7.
Contoh yang lainnya yaitu:
- 11+6=17
- 5+6=11
- 13+6=19
- 17+6, 23+6, dan seterusnya
Itulah beberapa bilangan prima dari 1 sampai 100, semoga bisa membantu Anda dalam belajar dan mengerjakan soal-soal bilangan prima di sekolah. Semoga informasi bilangan prima dari 1 sampai 100 dari www.ayoksinau.com bermanfaat banyak untuk Anda.