Kumpulan Rumus Trigonometri Serta Contoh Soal Dan Jawabannya

Oleh Diposting pada

Apa pengertian Trigonometri?

Trigonometri (dari bahasa Yunani trigonon = tiga sudut dan metro = mengukur) adalah sebuah cabang matematika yang berhadapan dengan sudut segi tiga dan fungsi Trigonometri kseperti sinus, cosinus, dan tangen.  Ada banyak aplikasi trigonometri salah satunya adalah teknik triangulasi yang digunakan dalam astronomi untuk menghitung jarak ke bintang-bintang terdekat, hal ini dalam geografi untuk menghitung antara titik tertentu, dan dalam sistem navigasi satelit.

Rumus-Trigonometri

Bidang lainnya yang menggunakan trigonometri termasuk astronomi (dan termasuk navigasi, di laut, udara, dan angkasa), teori musik, akustik, optik, analisis pasar finansial, elektronik, teori probabilitas, statistika, biologi, pencitraan medis/medical imaging farmasi, kimia, teori angka seismologi, meteorologi, oseanografi, berbagai cabang dalam ilmu fisika, survei darat dan geodesi, arsitektur, fonetika, ekonomi, teknik listrik, teknik mekanik, teknik sipil, grafik komputer, kartografi, kristalografi.

Trigonometri sendiri memiliki sejarah yang sangat menarik dipelajari. Sudah lebih dari 3000 tahun yang lalu trigonometri dikenal. Seorang matematikawan dari yunani yaitu Hipparchus menyusun tabel trigonometri untuk menyelesaikan segitiga. Selain itu juga Lagadha matematikawan yang sampai sekarang masih terkenal menghitung astronomi dengan menggunakan trigonometri dan geometri. Adapun beberapa kumpulan rumus trigonometri yang dapat dipelajari.

  • Apa fungsi Trigonometri?

Fungsi trigonometri adalah hal yang sangat penting dalam sains, teknik, arsitektur dan bahkan farmasi.

Kumpulan Rumus Trigonometri

Kumpulan-Rumus-Trigonometri

Sedangkan trigonometri terdiri dari sinus (sin), tangens (tan), cosinus (cos), contangens (cot), secan (sec), dan cosecan (cosec). Lebih lanjut mengenai persamaan trigonometri akan Anda pelajari pada uraian berikut.

1. Kumpulan rumus trigonometri Perbandingan Trigonometri

a. Kumpulan rumus trigonometri Jumlah dan Selisih dua Sudut

  • Rumus Cosinus jumlah selisih dua sudut

cos (A + B) = cos A cos B – sin A sin B cos
(A – B) = cos A cos B + sin A sin B

  • Rumus Sinus Jumlah dan Selisih Dua Sudut

sin (A + B) = sin A cos B + cos A sin B sin
(A – B) = sin A cos B – cos A sin B

  • Rumus Tangen Jumlah dan Selisih Dua Sudut

2. Kumpulan Rumus Trigonometri untuk sudut rangkap

  • Rumus sin (A+ B) untuk A = B, diperoleh:

sin 2A = sin (A + B)
= sin A cos A + cos A sin A
= 2 sin A cos A
Jadi,sin2A =2 sin A cos A

  • Rumus cos (A + B) untuk A = B,diperoleh:

cos 2A = cos (A + A)
= cos A cos A-sin A sin
A = cos2A-sin2A ……………(1)

Atau

Cos 2A = cos2A-sin2A
= (1 -sin2A)-sin2A
= 1 – 2 sin2A  ………. (3)

Dari persamaan (1) (2) (3) didapatkan rumus sebagai berikut.

Cos 2A = cos2 A – sin2 A
= 2 cos2 A-1
= 1 – 2 sin2 A

  • Dengan menggunakan rumus tan (A+B) untuk A=B,diperoleh

3. Kumpulan rumuh trigonometri Perkalian, Penjumlahan, dan Pengurangan Sinus dan Kosinus

  • Rumus Perkalian Sinus dan Kosinus

2 sin A sin B = cos (A- B) – cos (A+ B)
2 sin A cos B = sin (A + B) + sin (A-B)
2 cos A sin B = sin (A + B)-sin (A-B)
2 cos A cos B = cos (A + B) + cos (A- B)

  • Rumus Penjumlahan dan Pengurangan Sinus dan Kosinus

sin A + sin B = 2sin ½ (A+B) cos ½ (A-B)
sin A – sin B = 2cos ½ (A+B) sin ½ (A-B)
cos A + cos B = 2cos ½ (A+B) cos ½ (A-B)
cos A – cos B = -2sin ½ (A+B) cos ½ (A-B)

tan A + tan B =

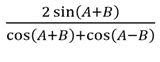
tan A – tan B =

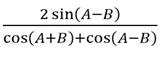
4. Kumpulan rumus trigonometri Identitas

Rumus rumus dasar identitas trigonometri sebagai berikut.

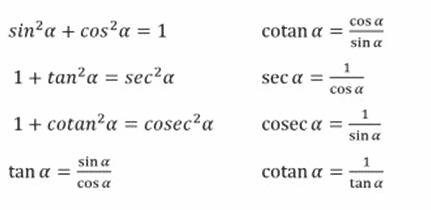
Tiap persamaan di atas, memuat perbandingan trigonometri dengan variable sudut x (dalam ukuran derajat dan radian).

  1. Penyelesaian persamaan sin x0 = sin ?0 (x ? R)

Untuk menyelesaiakan persamaan trigonometri sin x0 = sin ?0(x ? R) dapat ditentukan dengan menggunakan hubungan-hubungan yang berlaku pada perbandingan trigonometri sudut berelasi berikut.

  1. sin (1800-?0) = sin ?0
  2. sin (?o+k.3600) = sin ?0

Dengan menggunakan hubungan-hubungan di atas, maka penyelesaian persamaan trigonometri sin x0 = sin ?0 dapat ditetapkan sebagai berikut.

Jika sin x0 = sin ?0 (x ? R), maka:

x = ? + k.3600 atau x = (1800  ?  ?) + k.360, dengan k ? B

Catatan: x dalam derajat

Jika sin x = sin A (x ? R), maka:

x = A + k.2? atau x = (?  ?  A) + k.2?, dengan k ? B

Catatan: x dalam radian

Contoh:

  1. Tentukan penyelesaian dari tiap persamaan trigonometri berikut ini:
a.    sin x0 = sin 250 b.      sin x0 = sin 500

Jawab:

  1. sin x0 = sin 250, maka diperoleh:

x = 250 + k.3600     atau     x   = (1800  ?  250) + k.3600

= 1550 + k.3600

Jadi, x = 250 + k.3600 atau 1550 + k.3600

  1. sin x0 = sin500, maka diperoleh:

x = 500 + k.3600     atau     x   = (1800  ?  500) + k.3600

= 1300 + k.3600

Jadi, x = 500 + k.3600 atau 1300 + k.3600

  1. Tentukan himpunan penyelesaian dari tiap persamaan trigonometri berikut ini.
  2. sin 2x0 = sin 400, jika x dalam interval 0 ? x ? 3600
  3. sin 3x0 = sin 450, jika x dalam interval 0 ? x ? 3600

Jawab:

  1. sin 2x0 = sin 400, maka diperoleh:

2x = 400 + k.3600     atau     2x = (1800  ?  400) + k.3600

» x = 200 + k.3600                »   2x   = 1400 + k.3600

»   x     = 700 + k.3600

untuk   k = 0 ? x = 200     atau untuk    k = 0 ? x = 700

k = 1 ? x = 2000                        k = 1 ? x = 2500

Jadi, himpunan penyelesaiannya adalah HP = {200, 700, 2000, 2500}

  1. sin 3x0 = sin 450, maka diperoleh:

3x = 450 + k.3600     atau     3x = (1800  ?  4500) + k.3600

» x = 150 + k.3600    atau     »   3x   = 1350 + k.3600

»   x     = 450 + k.1200

untuk   k = 0 ? x = 150     atau untuk    k = 0 ? x = 450

k = 1 ? x = 1350                        k = 1 ? x = 1650

k = 2 ? x = 2550                        k = 2 ? x = 2850

Jadi, himpunan penyelesaiannya adalah:

HP = {150, 450, 1350, 1650, 2550, 2850}

Demikian kumpulan rumus trigonometri dari www.ayoksinau.com yang dapat dipelajari semoga bermanfaat .

Baca Juga :

Posting terkait: