
Pengertian Bilangan Rasional
Bilangan rasional (Q) adalah bilangan yang dapat dinyatakan dengan perbandingan (rasio)- , yang mana a adalah bilangan bulat, b adalah bilangan bulat b = 0. Bilangan yang bisa dinyatakan sebagai a/b dimana a/b bilangan bulat dan b tidak sama dengan 0. Batasan bilangan rasional yaitu mulai dari selanga. Bilangan dibagi menjadi dua yaitu bilangan rasional dan irasional. Bilangan rasional meliputi bilangan asli, bilangan bulat, bilangan prima, bilangan cacah, dan bilangan lain yang subset dengan bilangan rasional.
Bilangan rasional merupakan bilangan yang dapat dinyatakan dalam bentuk a/b dengan a dan b merupakan bilangan bulat serta b ? 0. Bilangan rasional dapat disebut juga sebagai bilangan pecahan. Dalam bilangan rasional berbentuk a/b, bilangan a melambangkan pembilang dan b merupakan penyebut bilangan rasional.
Himpunan yang anggota-anggota adalah semua bilangan rasional disebut himpunan bilangan rasional. Notasi himpunan bilangan rasional, yaitu :
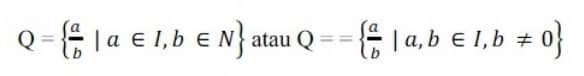
Keterangan
- Q : Bilangan rasional
- I : Bilangan bulat
- N : Bilangan asli
Bilangan rasional terdiri atas :
- Bilangan rasional bulat
Contoh. 12:3——- ? 12/3, yang artinya 4 sebab 4×3 = 12 - Bilangan rasional pecahan biasa
Contoh. 1/2 = 0,5 Sebab bilangan tersebut tidak dapat dinyatakan sebagai bilangan bulat. - Bilangan rasional pecahan campuran
Contoh. l 2/5= 1 + 2/5 Karena memuat bilangan bulat yaitu 1, dan bilangan pecahan 2/5 , maka disebut bilangan rasional pecahan campuran.
Baca Juga Artikel Yang Mungkin Berhubungan : Sistem Bilangan Biner (Pengertian Dan Contohnya)
Sejarah Bilangan Rasional
Sebelum mempelajari bilangan rasional, siswa telah dikenalkan dengan beberapa jenis bilangan, antara lain: bilangan asli, bilangan cacah, bilangan prima, bilangan bulat, bilangan pecahan atau pecahan, bilangan positif, bilangan negatif.
Mula-mula yang dikenal manusia adalah bilangan bulat positif, yaitu bilangan asli (natural numbers, N). Bilangan asli dibutuhkan manusia untuk membilang sesuatu yang utuh, seperti banyak orang, banyak hewan, dan semacamnya. Selanjutnya manusia mengenal bilangan pecahan (fractions) dengan berbagai macam bentuk. Di Mesir kuno dikenal dengan penyebut 1 atau 2 saja. Di Perancis kuno, dikenal dengan penyebut kelipatan 6 atau 12. Di bangsa-bangsa lain juga akhirnya mengenal pecahan dengan ragam bentuk yang berbeda-beda.
Mengenai bilangan prima (prime numbers), telah menjadi kajian intensif orang Yunani kuno, terutama pada perguruan Pythagoras. Mereka menemukan bahwa bilangan prima adalah “sumber bilangan asli” di mana semua bilangan asli dapat dinyatakan dalam faktorisasi prima.
Pada perkembangan selanjutnya, orang membutuhkan bilangan bertanda oleh karena kuantitas sesuatu dapat “berjalan” ke dua arah yang berlawanan. Misalnya untuk menjawab pertanyaan “berapa kambing yang dia punya?”. Padalah faktanya ia berutang 3 ekor kambing dan tidak memiliki kambing sama sekali. Daripada menjawab “tidak ada”, jawaban “negatif tiga” akan lebih masuk akal. Dipelopori Brahmagupta (598-670) dan juga al-Biruni (973-1048), penggunaan bilangan bertanda menjadi luas diterima orang.
Salah satu perkembangan penting kemampuan berhitung manusia adalah dimulainya penggunaan angka nol. Walaupun telah disinggung oleh bangsa Maya dan juga oleh matematikawan India-semisal Brahmagupta, tetapi konsep bilangan . nol (zero) dan penggunaan angka nol belum dipahami manusia hingga pengenalan dan penggunaan sistem desimal sekitar abad ke- 12 hingga abad ke-15. Di tangan matematikawan muslim, terutama al-Kashi (1380-1429), penulisan desimal menjadi trend. Dalam penulisan desimal ini, angka nol mutlak dibutuhkan. Muncullah kemudian angka dan bilangan nol.
Dengan bilangan nol, orang sekarang telah memiliki referensi untuk menjawab pertanyaan “berapa banyak … ?” Kita menyebutnya dengan istilah bilangan cacah (whole numbers). Ditambah pecahan, manusia telah memiliki pengetahuan dalam menyatakan semua kuantitas hasil pembagian bilangan bulat dengan bilangan asli.
Kemunculan Bilangan Rasional dari Sudut Pandang Matematis
Mula-mula dikenal bilangan asli. Apakah setiap bilangan asli dapat dinyatakan sebagai perkalian bilangan-bilangan lain? Ya, yaitu dengan satu dan jenis bilangan baru yang disebut bilangan prima.
Untuk 2 + … = 6 maka dapat ditemukan bilangan asli 4 untuk mengisi titik-titik. Tetapi bagaimana bila 2 + … = 2. Daripada menyebut bahwa tidak ada bilangan asli yang mengisi titik-titik, lebih baik kita memperluas jenis bilangan yang kita kenal. Muncullah bilangan nol.
Semua bilangan asli dan nol, kita golongkan sebagai himpunan bilangan cacah (whole numbers). Untuk mengisi titik-titik pada 3 + … = 2 kita memerlukan bilangan dengan “arah” yang berlawanan dari biasanya. Muncullah bilangan negatif.
Semua bilangan cacah dan bilangan negatifnya, kita golongkan sebagai himpunan bilangan bulat (integers) Selanjutnya, untuk menjawab 2 x … = 3 maka kita memerlukan jenis bilangan baru yang kita sebut pecahan. Dalam kasus ini, kita dapatkan pecahan dalam bentuk a/b dengan a dan b bilangan-bilangan bulat. Satu-satunya kasus di mana kita tidak menemukan adanya pecahan yang sesuai adalah kasus
0 x … = a dengan a sebarang bilangan bulat kecuali nol. Seperti bilangan bulat, pecahan-pun terdiri atas pecahan positif dan pecahan negatif. Nah, semua bilangan yang telah kita kenal hingga di sini, digolongkan menjadi satu jenis bilangan yang disebut bilangan rasional.
Baca Juga Artikel Yang Mungkin Berhubungan : Contoh Bilangan Cacah Lengkap
Struktur Himpunan Bilangan Rasional
Dengan mengikuti uraian sebelumnya, maka bilangan rasional dapat dinyatakan sebagai bilangan bulat atau pecahan yang dapat dinyatakan dalam bentuk biasa atau common fraction (terdiri atas pembilang dan penyebut). Himpunan bilangan rasional adalah gabungan semua bilangan bulat dan pecahan “biasa”. Lambang himpunan bilangan rasional adalah Q.
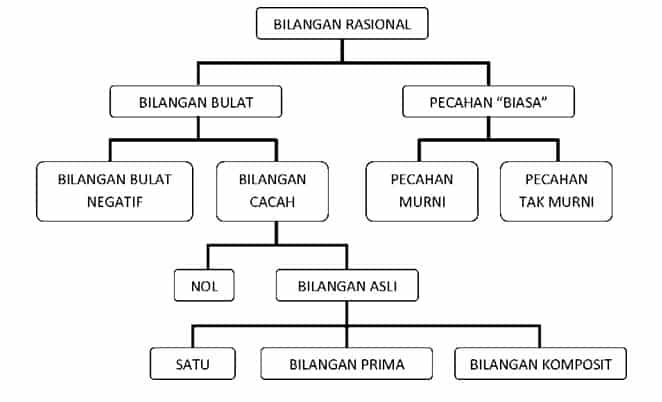
Keterangan :
Pecahan murni adalah pecahan dalam bentuk a/b dengan a < b.
Pecahan tak murni adalah pecahan dalam bentuk a/b dengan a > b.
Salah satu jenis pecahan murni adalah pecahan satuan (kadang disebut pecahan mesir). Pecahan satuan adalah pecahan biasa dengan pembilang 1. Seperti bilangan satu yang “membentuk” semua bilangan asli, maka pecahan satuan juga membentuk semua pecahan biasa.
Baca Juga Artikel Yang Mungkin Berhubungan : Macam Macam Bangun Ruang, Bentuk & Rumusnya | Ayoksinau.com
Sifat-sifat Bilangan Rasional
Secara umum bilangan rasional dan irasional mempunyai sifat yang hampir sama yaitu komutatif, asosiatif, distributif, mempunyai elemen identitas, setiap elemen punya invers, dan perkalian dengan 0. Satu sifat yang berbeda adalah bilangan irasional bersifat tidak tertutup.
Dengan menganggap setiap bilangan bulat sebagai sebuah “pecahan” dalam bentuk pecahan biasa dengan penyebut 1, maka sifat-sifat bilangan rasional “mengikuti” sifat-sifat pecahan biasa.
- Jika a, b, c, € I, b ? 0 dan c ? 0, maka a/b = a/b = ac/bc
Contoh : Bilangan rasional 3/4 dan bilangan bulat 5, 3/4 = 3.5/4.5 atau 3/4 = 15/20 - Jika a dan b mempunyai faktor persekutuan terbesar 1 maka bilangan rasional a/b disebut sederhana.
Contoh : Bilangan rasional 2/5 adalah sederhana sebab faktor persekutuan terbesar dari 2 dan 5 adalah 1 atau 2 relatif prima dengan 5.
Sifat-Sifat Operasi Bilangan Rasional
- Berlaku sifat-sifat terhadap operasi penjumlahan: identitas 0, tertutup, komutatif, asosiatif.
- Berlaku sifat-sifat terhadap operasi perkalian: identitas 1, tertutup, komutatif, asosiatif.
- Negatif dari suatu bilangan rasional adalah juga bilangan rasional.
- Kebalikan dari suatu bilangan rasional adalah juga sebuah bilangan rasional.
- Ketertutupan terhadap penjumlahan, perkalian, dan pengurangan;
- Komutatif terhadap penjumlahan dan perkalian;
- Asosiatif terhadap penjumlahan dan perkalian;
- Mempunyai elemen identitas 0 terhadap penjumlahan;
- Mempunyai elemen identitas 1 terhadap perkalian;
- Setiap elemen mempunyai lawan (invers penjumlahan);
- Kecuali 0, setiap elemen mempunyai kebalika (invers perkalian);
- Perkalian bersifat distributive terhadap penjumlahan.
Baca Juga Artikel Yang Mungkin Berhubungan : Info Lengkap Pengertian Stakeholder Dan Istilah Stakeholder | Ayok Sinau
Bilangan Rasional Desimal
Hubungan bilangan rasional dan bilangan desimal
- Notasi desimal yang diperluas melibatkana per sepuluhan, per seratusan, per seribuan, dan seterusnya.
- Bilangan rasional :per sepuluhan mempunyai satu angka disimal; per seratusan mempunyai dua angka desimal; per seriban mempunyai tiga angka desimal; dan seterusnya.
- Bilangan rasional dapat dinyatakan sebagai bilangan desimal dengan mengubah penyebut menjadi 10, 100, 1000, … atau dengan pembagian biasa.
- Dalam melakukan pembagian biasa, proses pembagian dapat berakhir atau dapat berulang.
- Bilangan rasional dapat dinyatakan sebagai desimal berakhir atau desimal berulang.
- Bilangan desimal berakhir atau bilangan desimal berulang salalu dapat dinyatakan sebagai bilangan rasional.
Mengubah Pecahan ke Desimal
Mengubah pecahan ke desimal bisa dilakukan dengan pembagian bersusun. Untuk pecahan dengan penyebut membagi habis bilangan kelipatan 10 caranya yaitu dengan mengalikan pembilang dan penyebut.
Perhatikan contoh: 3/5 = 3/5 x 2/2 = 6/10 = 0,6.
3/5 mempunyai penyebut 5 dan membagi habis bilangan kelipatan 10. Guna menghasilkan bilangan kelipatan 10 pada penyebut perlu mengali bilangan 5 dengan 2. Pembilangnya juga perlu dikali dengan bilangan 2 maka akan didapat 6/10. 10 menunjukkan banyak angka di belakang koma, sebab 10 adalah kelipatan ke 1 dari 10 maka angka di belakang koma pada desimal sebanyak satu angka. Pembilang pecahan tersebut yaitu 6, karena angka 6 hanya memiliki satu angka maka 6 menjadi satu-satunya angka di belakang koma.
Baca Juga Artikel Yang Mungkin Berhubungan : Contoh Bilangan Prima dari 1 Sampai 100 [TERLENGKAP]
Contoh dari Bilangan Rasional
- (a/b) = -a/b = a / -b dan (a/b)-1 = b/a jika a tidak sama dengan 0
- a/b : c/d = ad / bc
Bilangan rasional yakni bilangan yang bisa dinyatakan dalam bentuk a/b dengan a serta b adalah anggota bilangan bulat. Bilangan ini bisa dinyatakan dalam pecahan dan desimal. Banyak orang beranggapan bahwa bilangan desimal itu ada komanya, padahal tidak selalu seperti itu. Penulisan bilangan tunggal misalnya 7 juga merupakan penulisan desimal. Karena tanda koma digunakan untuk hasil pembagian dua buah bilangan yang mempunyai sisa ataupun guna keperluan ketelitian serta keperluan penulisan angka penting. Contoh bilangan rasional yaitu 2, 0.25, ¾, 1.333.. dan masih banyak lagi. Bilangan tadi merupakan anggota himpunan bilangan rasional sebab dapat dinyatakan dalam bentuk pecahan dan masing-masing pembilang serta penyebutnya adalah anggota bilangan bulat.
Bilangan 2 dapat dikatakan dalam bentuk pecahan 2/1, 0.25 menjadi ¼. Bilangan ¾ jelas berbentuk pecahan dengan 3 sebagai pembilang dan 4 sebagai penyebut dan keduanya adalah bilangan bulat. Bilangan 1.333 juga disebut bilangan rasional sebab dapat dinyatakan dalam pecahan 4/3. Sebelum membahas lebih jauh mengenai operasi bilangan rasional, maka harus pahami dahulu bagaimana cara mengubah penulisan bilangan rasional ke desimal juga sebaliknya.
- Angka 4. Angka ini dapat disusun ulang menjadi 4/1 .a = 4 dan b = 1. Jadi, 4 bilangan rasional.
- Pecahan 2/3. Pecahan ini jelas merupakan bilangan rasional, karena a=2 dan b=3.
- Pecahan 35/42. Ambil a=35 dan b=42. Jelas, bilangan ini merupakan bilangan rasional juga.
- Bagaimana dengan bilangan 0,98787768638?
Jawab: Tentu saja bilangan rasional. Itu khan bisa diubah menjadi 98787768638/10000000000.



