Pengertian dan Macam Himpunan beserta Contohnya

Pengertian Himpunan

Himpunan adalah (kumpulan objek yang memiliki sifat yg dapat didefinisikan dengan jelas) segala koleksi benda-benda tertentu yang dianggap sebagai satu kesatuan. Walaupun hal ini merupakan ide yang sederhana, tidak salah jika himpunan merupakan salah satu konsep penting dan mendasar dalam matematika modern, dan karenanya, studi mengenai struktur kemungkinan himpunan dan teori himpunan, sangatlah berguna.

Konsep himpunan mendasari hampir semua cabang matematika. Gerorg Cantor dianggap sebagai Bapak teori himpunan. Himpunan adalah kumpulan benda atau objek-objek atau lambang-lambang yang mempunyai arti yang dapat didefinisikan dengan jelas mana yang merupakan anggota himpunan dan mana bukan anggota himpunan. Istilah didefinisikan dengan jelas dimaksukkan agar orang dapat menentukan apakah suatu benda merupakan anggota himpunan yang dimaksud tadi atau tidak.

Perhatikan objek yang berada di sekeliling kita, misal ada sekelompok mahasiswa yang sedang belajar di kelas A, setumpuk buku yang berada di atas meja belajar, sehimpunan kursi di dalam kelas A, sekawanan itik berbaris menuju sawah, sederetan mobil yang antri karena macet dan sebagainya, semuanya merupakan contoh himpunan dalam kehidupan sehari-hari.

Jika kita amati semua objek yang berada disekeliling kita yang dijadikan contoh di atas, dapat didefinisikan dengan jelas dan dapat dibedakan mana anggota himpunan tersebut dan mana yang bukan.Himpunan makanan yang lezat, himpunan gadis yang cantik dan himpunan bunga yang indah adalah contoh himpunan yang tidak dapat didefinisikan dengan jelas. Lezatnya makanan, cantiknya gadis dan indahnya bunga bagi setiap orang relatif. Lezatnya suatu hidangan bagi seseorang atau sekelompok orang belum tentu lezat bagi orang lain atau sekelompok orang lainya.

Demikian juga indahnya sekuntum bunga bagi seseorang belum tentu indah bagi orang lain. Bagi A yang indah adalah mawar merah bagi B yang indah adalah melati. Jadi relatif bagi setiap orang. Benda atau objek yang termasuk dalam himpunan disebut anggota atau elemen atau unsur himpunan tersebut. Umumnya penulisan himpunan menggunakan huruf kapital A, B, C dan seterusnya, dan anggota himpunan ditulis dengan huruf kecil.

Baca Juga Artikel Yang Mungkin Berhubungan : Contoh Bilangan Cacah Lengkap

Notasi Himpunan

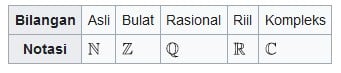
Biasanya, nama himpunan ditulis menggunakan huruf besar, misalnya S, A, atau B, sementara anggota himpunan ditulis menggunakan huruf kecil (a, c, z). Cara penulisan ini adalah yang umum dipakai, tetapi tidak membatasi bahwa setiap himpunan harus ditulis dengan cara seperti itu. Tabel di bawah ini menunjukkan format penulisan himpunan yang umum dipakai.

Himpunan-himpunan bilangan yang cukup dikenal, seperti bilangan kompleks, riil, bulat, dan sebagainya, menggunakan notasi yang khusus.

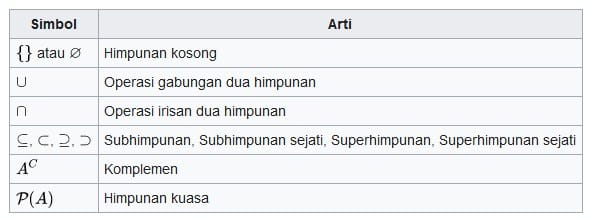
Simbol-simbol khusus yang dipakai dalam teori himpunan adalah:

Himpunan dapat didefinisikan dengan dua cara, yaitu:

a. Enumerasi, yaitu mendaftarkan semua anggota himpunan. Jika terlampau banyak tetapi mengikuti pola tertentu, dapat digunakan elipsis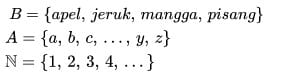

b. Pembangun himpunan, tidak dengan mendaftar, tetapi dengan mendeskripsikan sifat-sifat yang harus dipenuhi oleh setiap anggota himpunan tersebut.

Notasi pembangun himpunan dapat menimbulkan berbagai paradoks, contohnya adalah himpunan berikut:

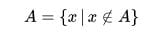
Himpunan A tidak mungkin ada, karena jika A ada, berarti harus mengandung anggota yang bukan merupakan anggotanya. Namun jika bukan anggotanya, lalu bagaimana mungkin A bisa mengandung anggota tersebut.

Baca Juga Artikel Yang Mungkin Berhubungan : Macam Macam Bangun Ruang

Jenis dan Macam Himpunan

Himpunan Bagian (Subset).

Himpunan A dikatakan himpunan bagian (subset) dari himpunan B ditulis A ? B ”, jika setiap anggota A merupakan anggota dari B.
Syarat :

A ? B, dibaca : A himpunan bagian dari B
A ? B, dibaca : A bukan himpunan bagian dari B
B ? A dibaca : B bukan himpunan bagian dari A
B ? A dibaca : B bukan himpunan bagian dari A

Contoh :
Misal A = { 1,2,3,4,5 } dan B = { 2,4} maka B ? A
Sebab setiap elemen dalam B merupakan elemen dalam A, tetapi tidak sebaliknya.
Penjelasan : Dari definisi diatas himpunan bagian harus mempunyai unsur himpunan A juga merupakan unsur himpunan B.artinya kedua himpunan itu harus saling berkaitan

Himpunan Kosong (Nullset)

Himpunan kosong adalah himpunan yang tidak mempunyai unsur anggota yang sama sama sekali.
Syarat :

Himpunan kosong = A atau { } Himpunan kosong adalah tunggal
Himpunan kosong merupakan himpunan bagian dari setiap himpunan

Perhatikan : himpunan kosong tidak boleh di nyatakan dengan { 0 }.
Sebab : { 0 } ? { }
Penjelasan : dari definisi diatas himpunan kosong adalah himpunan yang tidak mempunyai satupun anggota, dan biasanya himpunan kosong dinotasikan dengan huruf yunani ø (phi).

Himpunan Semesta

Himpunan semesta biasanya dilambangkan dengan “U” atau “S” (Universum) yang berarti himpunan yang memuat semua anggota yang dibicarakan atau kata lainya himpunan dari objek yang sedang dibicarakan.

Himpunan Sama (Equal)

Bila setiap anggota himpunan A juga merupakan anggota himpunan B, begitu pula sebaliknya.di notasikan dengan A=B
Syarat : Dua buah himpunan anggotanya harus sama.
Contoh :
A ={ c,d,e} B={ c,d,e } Maka A = B
Penjelasan : Himpunan equal atau himpunan sama,memiliki dua buah himpunan yang anggotanya sama misalkan anggota himpunan A {c,d,e} maka himpunan B pun akan memiliki anggota yaitu { c,d,e }.

Himpunan Lepas

Himpunan lepas adalah suatu himpunan yang anggota-anggotanya tidak ada yang sama.
Contoh C = {1, 3, 5, 7} dan D = {2, 4, 6} Maka himpunan C dan himpunan D saling lepas.
Catatan : Dua himpunan yang tidak kosong dikatakan saling lepas jika kedua himpunan itu tidak mempunyai satu pun anggota yang sama

Himpunan Komplemen (Complement set)

Himpunan komplemen dapat di nyatakan dengan notasi AC . Himpunan komplemen jika di misalkan S = {1,2,3,4,5,6,7} dan A = {3,4,5} maka A ? U. Himpunan {1,2,6,7} juga merupakan komplemen, jadi AC = {1,2,6,7}. Dengan notasi pembentuk himpunan ditulis : AC = {x?x ? U, x ? A}

Himpunan Ekuivalen (Equal Set)

Himpunan ekuivalen adalah himpunan yang anggotanya sama banyak dengan himpunan lain.
Syarat : Bilangan cardinal dinyatakan dengan notasi n (A) A?B, dikatakan sederajat atau ekivalen, jika himpunan A ekivalen dengan himpunan B,

Contoh :

A = { w,x,y,z }?n (A) = 4
B = { r,s,t,u } ?n (B) = 4
Maka n (A) =n (B) ?A?B

Penjelasan : himpunan ekivalen mempunyai bilangan cardinal dari himpunan tersebut, bila himpunan A beranggotakan 4 karakter maka himpunan B pun beranggotakan 4.

Baca Juga Artikel Yang Mungkin Berhubungan : Kumpulan Rumus Trigonometri Serta Contoh Soal Dan Jawabannya

Cara Penulisan Himpunan

Ada empat cara untuk menyatakan suatu himpunan

1. Dengan menyebutkan semua anggotanya (roster) yang diletakkan di dalam sepasang tanda kurung kurawal, dan di antara setiap anggotanya dipisahkan dengan tanda koma. Cara ini disebut juga cara Tabulasi.
Contoh: A = {a, i, u, e, o}
B = {Senin, Selasa, Rabu, Kamis, Jumat, Sabtu, Minggu}

2. Menyebutkan syarat anggota-anggotanya, cara ini disebut juga cara Deskripsi.
Contoh: ambil bilangan asli kurang dari 5
A = bilangan asli kurang dari 5

3. Notasi Pembentuk Himpunan : dengan menuliskan ciri umum atau sifat umum (role) dari anggotanya.
Contoh Soal :
Nyatakan dengan notasi himpunan dengan menuliskan tiap-tiap anggotanya dan sifat-sifatnya himpunan berikut :
A adalah himpunan bilangan asli antara 1 dan 6
Penyelesaian :
A adalah himpunan bilangan asli antara 1 dan 6
Dengan menulis tiap-tiap anggotanya A = {2, 3, 4, 5}
Dengan menulis sifat-sifatnya A = {x | 1 < x < Asli}Î6, x

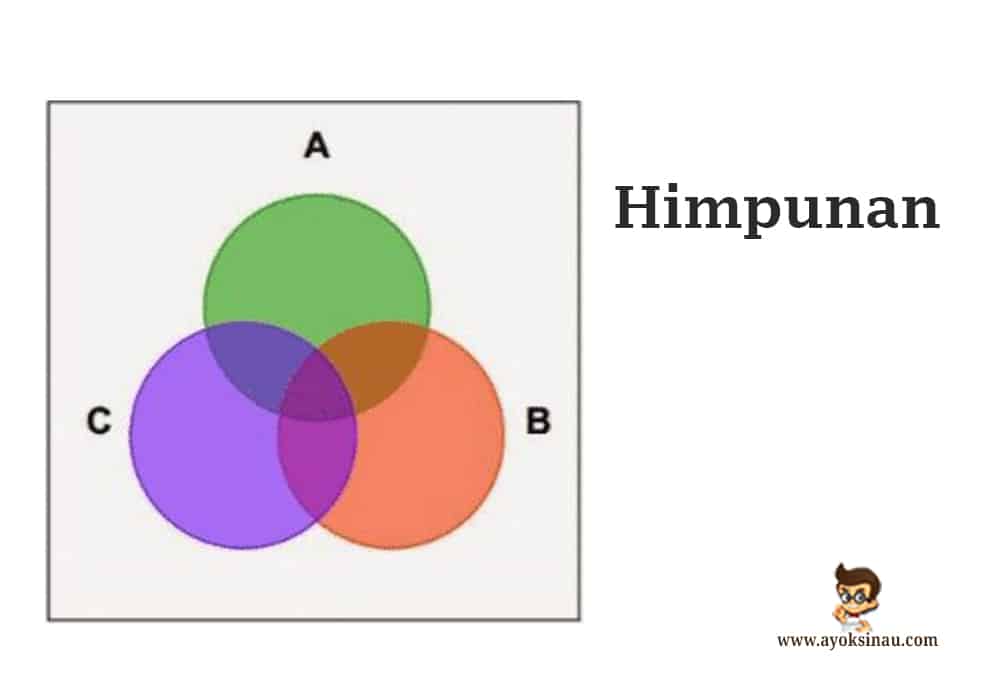
4. Himpunan juga dapat di sajikan secara grafis (Diagram Venn)
Penyajian himpunan dengan diagram Venn ditemukan oleh seorang ahli matematika Inggris bernama John Venn tahun 1881. Himpunan semesta digambarkan dengan segiempat dan himpunan lainnya dengan lingkaran di dalam segiempat tersebut.

Baca Juga Artikel Yang Mungkin Berhubungan : Sistem Bilangan Biner

Operasi Pada Himpunan

Gabungan
Gabungan (union) dari himpunan A dan B adalah himpunan yang setiap anggotanya merupakan anggota himpunan A atau himpunan B. Dinotasikan A B Notasi : A B = {x | x ? A atau x ? B}
Irisan
Irisan (intersection) dari himpunan A dan B adalah himpunan yang setiap anggotanya merupakan anggota dari himpunan A dan anggota himpunan B.
Notasi : A B = {x | x ? A dan x ? B}
Komplemen
Komplemen himpunan A terhadap himpunan semesta S adalah himpunan yang anggotanya merupakan anggota S yang bukan anggota A. Dinotasikan Ac
Notasi : Ac = {x | x ? S dan x ? A} atau
Selisih
Selisih himpunan A dan B adalah himpunan yang anggotanya merupakan anggota himpunan A dan bukan anggota himpunan B. Selisih himpunan A dan B adalah komplemen himpunan B terhadap himpunan A. Dinotasikan A-B
Notasi : A – B = {x | x ? A dan x ? B}
Hasil Kali Kartesius ( cartesion Product )
Hasil kali kartesius himpunan A dan B, dinotasikan A x B, adalah himpunan yang anggotanya semua pasangan terurut (a,b) dimana a anggota A dan b anggota B
Secara matematis dituliskan : A x B = {(a,b)| a ? A dan b ? B}

Hukum Aljabar Himpunan

Hukum-hukum pada himpunan dinamakan Hukum –hukum aljabar himpunan. cukup banyak hukum yang terdapat pada aljabar himpunan , tetapi disini hanya dijabarkan 11 saja. Beberapa hukum tersebut mirip dengan hukum aljabar pada sistem bilangan riil seperti a (b+c) = ab + ac , yaitu hukum distributif.

Hukum identitas:
A = A
A U = A
Hukum null/dominasi:
A =
A U = U
Hukum komplemen:
A = U
A =
Hukum idempoten:
A A = A
A A = A
Hukum involusi:
= A
Hukum penyerapan (absorpsi):
A (A B) = A
A (A B) = A
Hukum komutatif:
A B = B A
A B = B A
Hukum asosiatif:
A (B C) = (A B) C
A (B C) = (A B) C
Hukum distributif:
A (B C) = (A B) (A C)
A (B C) = (A B) (A C)
Hukum De Morgan:
=
=
Hukum 0/1
= U
= Æ

Terlihat bahwa hukum- hukum yang berlaku pada himpunan merupakan analogi hukum –hukum logika , dengan operator menggantikan L (dan) , sedangkan operator menggantikan V ( atau ).

Baca Juga Artikel Yang Mungkin Berhubungan : 5 Cara Menghitung Cepat Matematika [CARA NO 1 SIMPEL BANGET]

Contoh Himpunan

Himpunan Berhingga (finite set) himpunan yg unsurnya bila di hitung akan di peroleh jumlahnya.
Contoh :
P : himpunan bulan dalam setahun
Q : Himpunan siswa dalam satu kelas
Himpunan Tak Berhingga (Infinet set) himpunan yg unsurnya bila di hitung tidak akan di peroleh hasilnya sampai kita berhenti menghitungnya.
Contoh :
R : Himpunan bilangan cacah {0,1,2…}
Himpunan Kosong (Hampa) adalah Himpunun yg tidak memiliki anggota sama sekali.
Contoh :
Kuda bermata 3. Alasan pada umumnya kuda bermata 2
Himpunan Semesta usaha untuk menyatakan sekumpulan objek yang merupakan bagian dari kumpulan objek-objeck tertentu tetapi memiliki batasan tertentu.
Contoh :
Himpunan warga di salah satu negara bagian Amerika Selatan maka di sini kita memiliki batasan dalam membahas himpunan tersebut. Dan secara keseluruhan warga negara di bagian Amerika Selatan adalah sebagian dari warga negara Amerika Lambang S atau U.
Himpunan Sederajat adalah himpunan dua buah himpunan yang memiliki jumlah bilangan kardinal yang sama.
Contoh :
R = { Putih, biru, merah, kuning}
S = { Rakit, Sampan, Perahu, Kapal }
N ( R ) = 4
N ( S) = 4
Himpunan Kuasa suatu pengelompokan himpunan yang dapat di bedakan dgn jalas anggotanya.
Contoh :
A{a,b,c)maka ini adalah himpunanya
{{a,b,c},{a,b},{a,c},{b,c},{a},{b},{c}}
Dimana n (2A) = 23 = 8
Himpunan bagian ada 2 yaitu suatu himpunanan A juga merupakan
himpunan B.
Notasinya : A C B
Himpunan bagian A di sebut himpunan murni dan himpunan B paling sedikit harus ada 1 unsur yang bukan unsur A.
Contoh :
A {2,4,6,8}
B {2,4,6,8,1}
Himpunan S juga termasuk himpunan R.
Contoh :
S {6,8,10,12}
R {6,8,10}
Notasinya : R C S
Dan jika suatu himpunan tidak memikiki unsur di sebut himpunan kosong.